There are many fields that I find fascinating, but one trend among them is that they often include some kind of applied mathematics. Neural networks are a particularly good example of this. I’ve also always enjoyed signal processing & controls theory, so on a whim I took a classed called Dynamic Optimization.

This course ended up being one of the most interesting and challenging of my college career. Centered around optimal control, the course applied mathematics in ways I never thought of, seamlessly integrating theoretical math and hardcore computation. Classical problems would be launching a rocket into orbit, intercepting a missile with a projectile, shortest path through an obstacle field, and so on - anything that contains controls.

The starting point for an optimal control problem is to satisfy the following conditions, derived from Pontryagin’s minimum principal and calculus of variations, and stolen from the class notes:

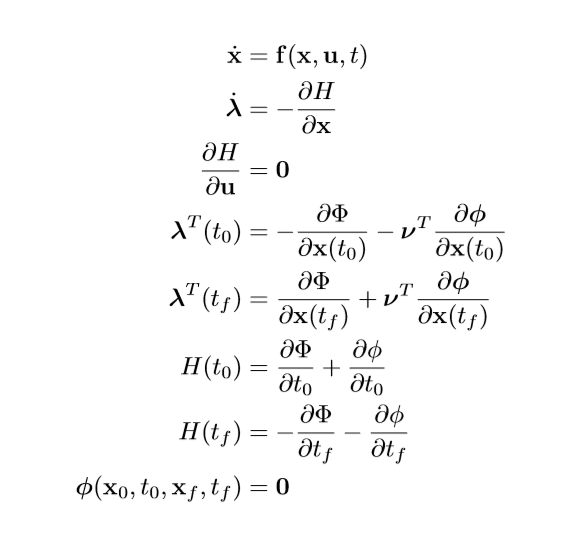
These few equations are some of the deepest math I’ve gone into and I loved every second of it. A fantastic resources is located here

Final Project

Anyway, the class wrapped up with a final project of our choosing. In the end, I chose to do “optimal moon landing”, where the goal is to minimize the time it takes to land on the moon in a rocket, given a set amount of fuel to start and end with. The write-up is located here. It was written in IEEE-ish format, but much more casually.

For the project, I ended up not being able to analytically derive a solution, but found a solution computationally. This result was quite interesting and seems common in the field. These problems are so large and complex that sometimes one might run into an integral that just cannot be done, or find a set of equations with infinite solutions.

I greatly enjoyed the project and the course and I hope to someday work with it more. It combines some of my favorite subjects - controls, optimization, and programming. In the write-up, I mention that I looked deeply at some other topics. In particular, I was highly interested in work similar to that done with spiking neurons or possibly, with even more ambition, optimal training of neural networks. Unfortunately, at this time, I was extremely overloaded with work to finish my degree, so I chose a project that was a bit easier… perhaps I will look at these things in the future!